Send
Close Add comments:
(status displays here)
Got it! This site uses cookies. You consent to this by clicking on "Got it!" or by continuing to use this website.nbsp; Note: This appears on each machine/browser from which this site is accessed.
Intractable problems
1. Intractable problems
2. Intractable problems
3. Intractable problems
An intractable problem requires exponential space, or time, or both.
That is, for a problem size of n, the time required would be exponential in n, or the space required would be exponential in n.
No amount of computer power will allow reasonable problems sizes of intractable problems to be solved.
4. Traveling salesman problem
An instance of the intractable
TSP (
Traveling Salesman Problem) goes as follows.
A salesman needs to visit 60 cities.
There is a cost to travel between each pair of cities.
Find the round trip that minimizes the cost of visiting each city exactly once.
How many ways are there to visit each city exactly once?
5. The number of trips
6. Number of trips
A salesperson is to plan a trip that visits each of n different cities such that the travel cost is minimized.
Start in one of the cities (1st city).
How many choices for the 2nd city? n-1.
How many choices for the 3nd city? n-2.
How many choices for the 4th city? n-3.
How many choices for the n-1 city? 1.
How many possible ways are there?
7. The factorial function
The
factorial function is defined as follows.
n! = n * (n-1) * (n-2) * ... * 1
(n-1)! = (n-1) * (n-2) * (n-3) * ... 3 * 2 * 1
The number of
permutations of
n objects is
n! (
n-factorial).
8. 7 factorial
9. 3 cities
10. 4 cities
11. 5 cities
12. 6 cities
13. 7 cities
14. 8 cities
15. 9 cities
16. 10 cities
17. 11 cities
18. 12 cities
19. Existence of solutions
There is obviously a tour that is no more expensive than any of the other tours.
20. Effective method
Check each possible route and find the one with minimum cost. Algorithm:
For Each possible route Do
calculate the cost of the route
If the cost is less than the least cost
found so far Then
Save this route (and cost), replacing any
previously saved route (and cost)
EndIf
End
21. Efficient method
No one knows an efficient way to get the best solution.
There are methods that can efficiently get close to the optimal solution.
22. Applications
The TSP has several applications even in its purest formulation, such as planning, logistics, and the manufacture of microchips. Slightly modified, it appears as a sub-problem in many areas, such as DNA sequencing. Wikipedia
23. Intractable problems
If there are 60 cities, there are 59! possible routes to check. 59! is about 1080.
1080, about 2270, is more than the number of small particles (protons, neutrons, electrons, etc.) in the known universe.
There is no known solution to the TSP that is efficient.
But, no one has been able to prove that there is not an efficient solution.
24. Small probabilities
25. Small probabilities
Most people are not used to working with low probabilities.
The number of small particles in the universe is 2270.
The number of seconds in 40 billion years in 260.
The number of millionths of seconds in 40 billion years in 280.
Remember the train puzzle? The math view ignores reality. The engineering view takes into account reality.
26. NP-complete problems
NP-complete problems are related to the TSP in that a solution, once found, is easy to verify.
Minesweeper is NP-complete!
27. Vertex cover
Vertex cover is NP-complete.
28. NP-hard
NP-hard problems are intractable, but not directly related to the TSP.
Factoring of numbers is an important security problem that is NP-hard.
29. Factorization
What is the factorization of 28?
The factorization if 28 is 2*2*7.
But, no one knows an efficient way to factor very large numbers.
No one knows if there is an efficient way, or whether there is not an efficient way.
30. Related problems
There are hundreds (even thousands) of practical problems that have been shown to be similar to the TSP in that if you can solve any one of them efficiently, you can solve all of them efficiently.
31. Examples of TSP problems
32. Exponential growth
traveling salesman problem
NP hard problems
fixed threshold problems
33. Practical problems
scheduling
best mix
shop scheduling
make-span scheduling
bin packing
covering problems
integer programming
34. Linear programming
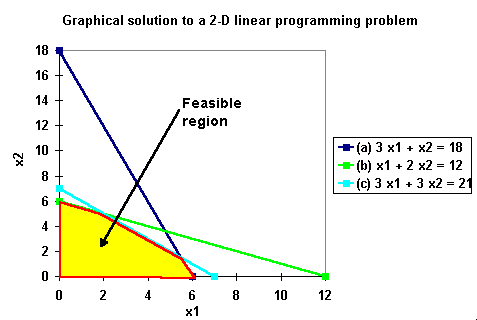
Linear programming is intractable in theory, but in practice, most problems are solved rapidly using the simplex method for linear programming.
35. Impossibility of testing
Exhaustive enumeration involves looking at every possible alternative. Suppose that you must determine whether a routine to multiply two 32 bit numbers is correct. You decide to do this by exhaustive enumeration. How long will this take? (Many floating point, or real, numbers contain 64 to 80 bits). Well, there are
2
32 * 2
32 = 2
64 possibilities.
Assume we can compute and check 1 million operations per second (about 2
20 operations per second). How long does it take? A rule to remember is that there are π seconds in a nano-century (10
9 century).
A problem is considered practically impossible if a computer with as many states as there are electrons in the known universe could not solve the problem (enumerate every possibility) if it were running at the speed of light for the known age of the universe.
36. End of page
37. Acronyms and/or initialisms for this page
1 acronyms omitted (login required)
