Send
Close Add comments:
(status displays here)
Got it! This site uses cookies. You consent to this by clicking on "Got it!" or by continuing to use this website.nbsp; Note: This appears on each machine/browser from which this site is accessed.
Associativity for expressions and trees
1. Associativity for expressions and trees
2. Associativity
Associativity in mathematics means that the order of the parentheses does not matter. The following are equivalent (infix) expressions.
w + (x + (y + z))
w + ((x + y) + z)
(w + x) + (y + z)
(w + (x + y)) + z
((w + x) + y) + z
Consider these expressions in postfix tree form.
3. Way 1
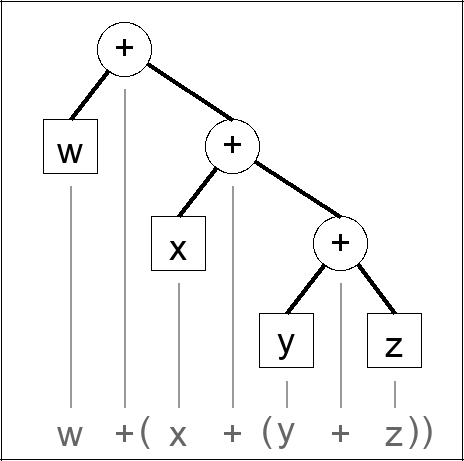
Infix:
w + (x + (y + z))
Postfix:
w x y z + + +
4. Way 2

Infix:
w + ((x + y) + z)
Postfix:
w x y z + + +
5. Way 3
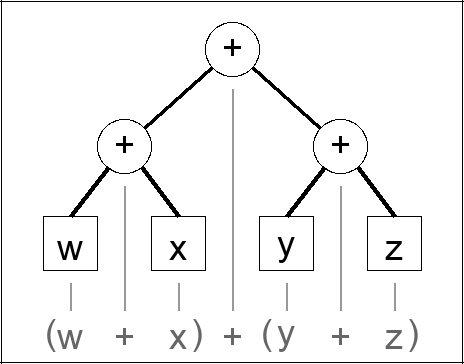
Infix:
(w + x) + (y + z)
Postfix:
w x y z + + +
6. Way 4
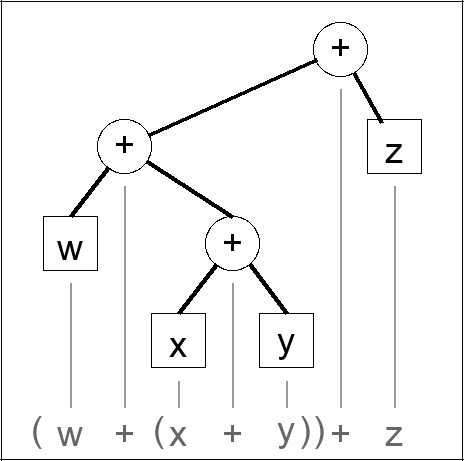
Infix:
(w + (x + y)) + z
Postfix:
w x y z + + +
7. Way 5

Infix:
((w + x) + y) + z
Postfix:
w x y z + + +
8. Parentheses
Note that parentheses are used to show precedence of operations, but disappear in the tree as they can be put in if needed in the output.
All of the postfix traversals result in the exact same form (or code).
9. End of page